Naive glmnet fitting procedure

naive_glmnet(
  x1,
  x2,
  y1,
  y2,
  s = "lambda.min",
  family = "binomial",
  z1,
  z2,
  ...
)

Arguments

x1: A data matrix of size n (number of samples) times p (number of features)
x2: A data matrix of size n (number of samples) times p (number of features)
y1: A vector
y2: A vector
s: Default to "lambda.min"
family: family of glmnet
z1: (Deprecated) a data matrix, columns are pairwise-differences between the original data columns.
z2: (Deprecated) a data matrix, columns are pairwise-differences between the original data columns.
...: Extra parameter settings for cv.glmnet

Value

A vector

Examples

data(cpop_data_binary, package = 'CPOP')
## Loading simulated matrices and vectors
x1 = cpop_data_binary$x1
x2 = cpop_data_binary$x2
y1 = cpop_data_binary$y1
y2 = cpop_data_binary$y2
set.seed(1)
cpop_result = cpop_model(x1 = x1, x2 = x2, y1 = y1, y2 = y2, alpha = 1, n_features = 10)
#> Absolute colMeans difference will be used as the weights for CPOP
#> Fitting CPOP model using alpha = 1
#> Based on previous alpha, 0 features are kept 
#> CPOP1 - Step 01: Number of selected features: 0 out of 190
#> CPOP1 - Step 02: Number of selected features: 9 out of 190
#> CPOP1 - Step 03: Number of selected features: 16 out of 190
#> 10 features was reached. 
#> A total of 16 features were selected. 
#> Removing sources of collinearity gives 13 features. 
#> 10 features was reached. 
#> A total of 13 features were selected. 
#> CPOP2 - Sign: Step 01: Number of leftover features: 9 out of 13
#> The sign matrix between the two data:
#>     
#>      -1 0 1
#>   -1  0 0 1
#>   0   0 0 0
#>   1   3 0 0
#> CPOP2 - Sign: Step 02: Number of leftover features: 8 out of 13
#> The sign matrix between the two data:
#>     
#>      -1 0 1
#>   -1  0 0 0
#>   0   0 0 0
#>   1   1 0 0
#> CPOP2 - Sign: Step 03: Number of leftover features: 8 out of 13
#> The sign matrix between the two data:
#>     
#>      -1 0 1
#>   -1  0 0 0
#>   0   0 0 0
#>   1   0 0 0
lasso_result = naive_glmnet(x1 = x1, x2 = x2, y1 = y1, y2 = y2, alpha = 1, intercept = FALSE)
cpop_result
#> CPOP model with  8 features 
#> # A tibble: 9 × 3
#>   coef_name    coef1    coef2
#>   <chr>        <dbl>    <dbl>
#> 1 (Intercept)  0      0      
#> 2 X01--X10    -0.322 -0.246  
#> 3 X09--X17     0.722  0.521  
#> 4 X11--X14     0.130  0.00292
#> 5 X12--X20     0.404  0.170  
#> 6 X01--X07    -0.437 -0.408  
#> 7 X01--X15    -0.158 -0.334  
#> 8 X01--X17    -0.901 -0.644  
#> 9 X04--X12     0.353  0.431  
lasso_result
#> $cpop_mode
#> [1] "glmnet"
#> 
#> $model1
#> 
#> Call:  glmnet::cv.glmnet(x = z1, y = y1, family = family, alpha = 1,      intercept = FALSE) 
#> 
#> Measure: Binomial Deviance 
#> 
#>      Lambda Index Measure      SE Nonzero
#> min 0.02765    54  0.7032 0.09817      14
#> 1se 0.09267    28  0.7935 0.05895       7
#> 
#> $model2
#> 
#> Call:  glmnet::cv.glmnet(x = z2, y = y2, family = family, alpha = 1,      intercept = FALSE) 
#> 
#> Measure: Binomial Deviance 
#> 
#>      Lambda Index Measure      SE Nonzero
#> min 0.03627    49  0.7289 0.09643      12
#> 1se 0.09195    29  0.8213 0.07194       9
#> 
#> $coef_tbl
#> $coef_tbl[[1]]
#> # A tibble: 191 × 3
#>    coef_name     coef1   coef2
#>    <chr>         <dbl>   <dbl>
#>  1 (Intercept)  0       0     
#>  2 X01--X02    -0.0922 -0.0930
#>  3 X01--X03     0       0     
#>  4 X01--X04    -0.502  -1.07  
#>  5 X01--X05    -0.0663  0     
#>  6 X01--X06     0      -0.0877
#>  7 X01--X07     0       0     
#>  8 X01--X08     0      -0.311 
#>  9 X01--X09    -0.893  -0.269 
#> 10 X01--X10    -0.0945  0     
#> # … with 181 more rows
#> 
#> 
#> attr(,"class")
#> [1] "naive_glmnet" "list"        
plot_cpop(cpop_result)
#> $plot

#> 
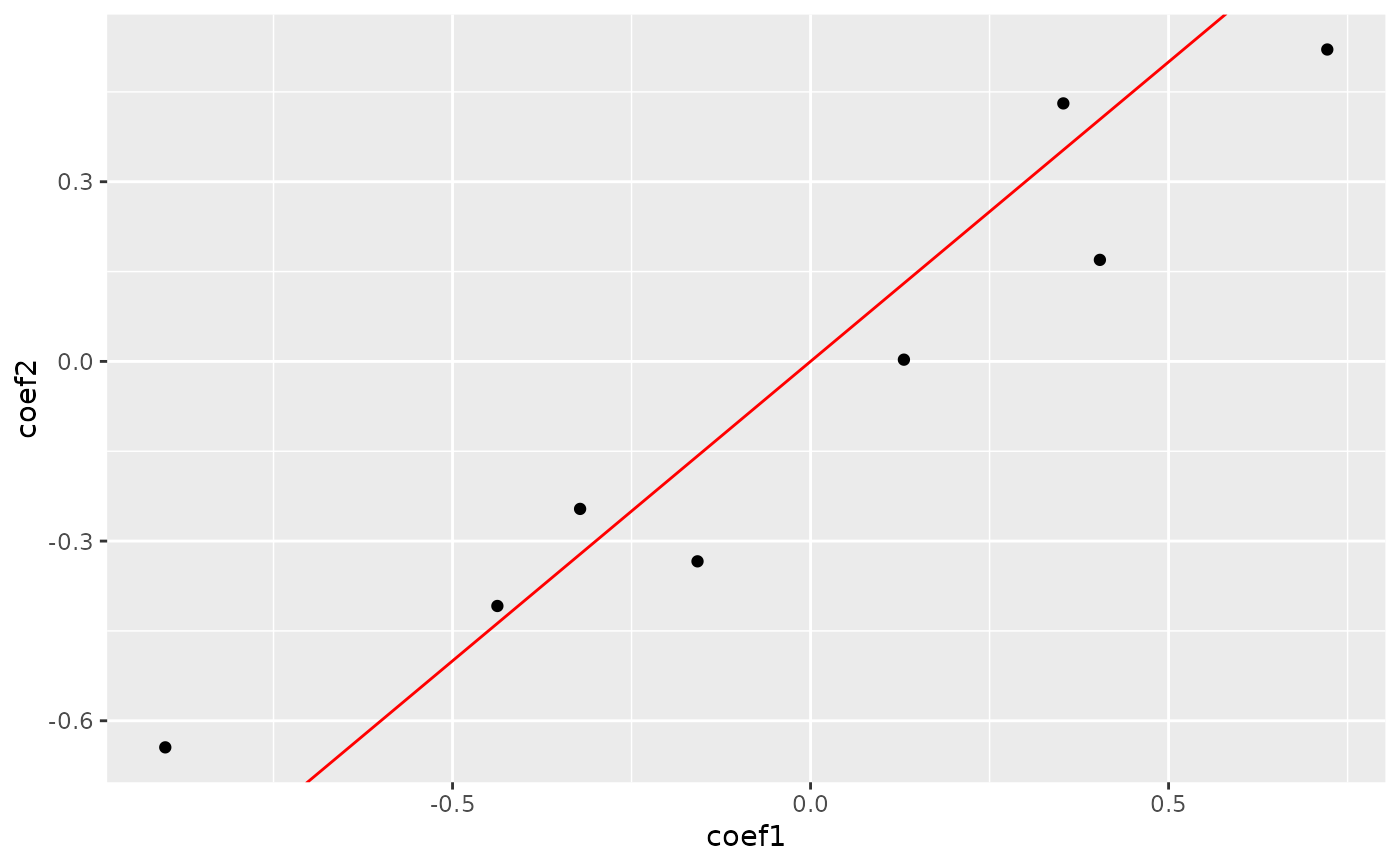#> $data
#> # A tibble: 8 × 3
#>   coef_name  coef1    coef2
#>   <fct>      <dbl>    <dbl>
#> 1 X01--X10  -0.322 -0.246  
#> 2 X09--X17   0.722  0.521  
#> 3 X11--X14   0.130  0.00292
#> 4 X12--X20   0.404  0.170  
#> 5 X01--X07  -0.437 -0.408  
#> 6 X01--X15  -0.158 -0.334  
#> 7 X01--X17  -0.901 -0.644  
#> 8 X04--X12   0.353  0.431  
#> 
plot_cpop(lasso_result)
#> $plot

#> 
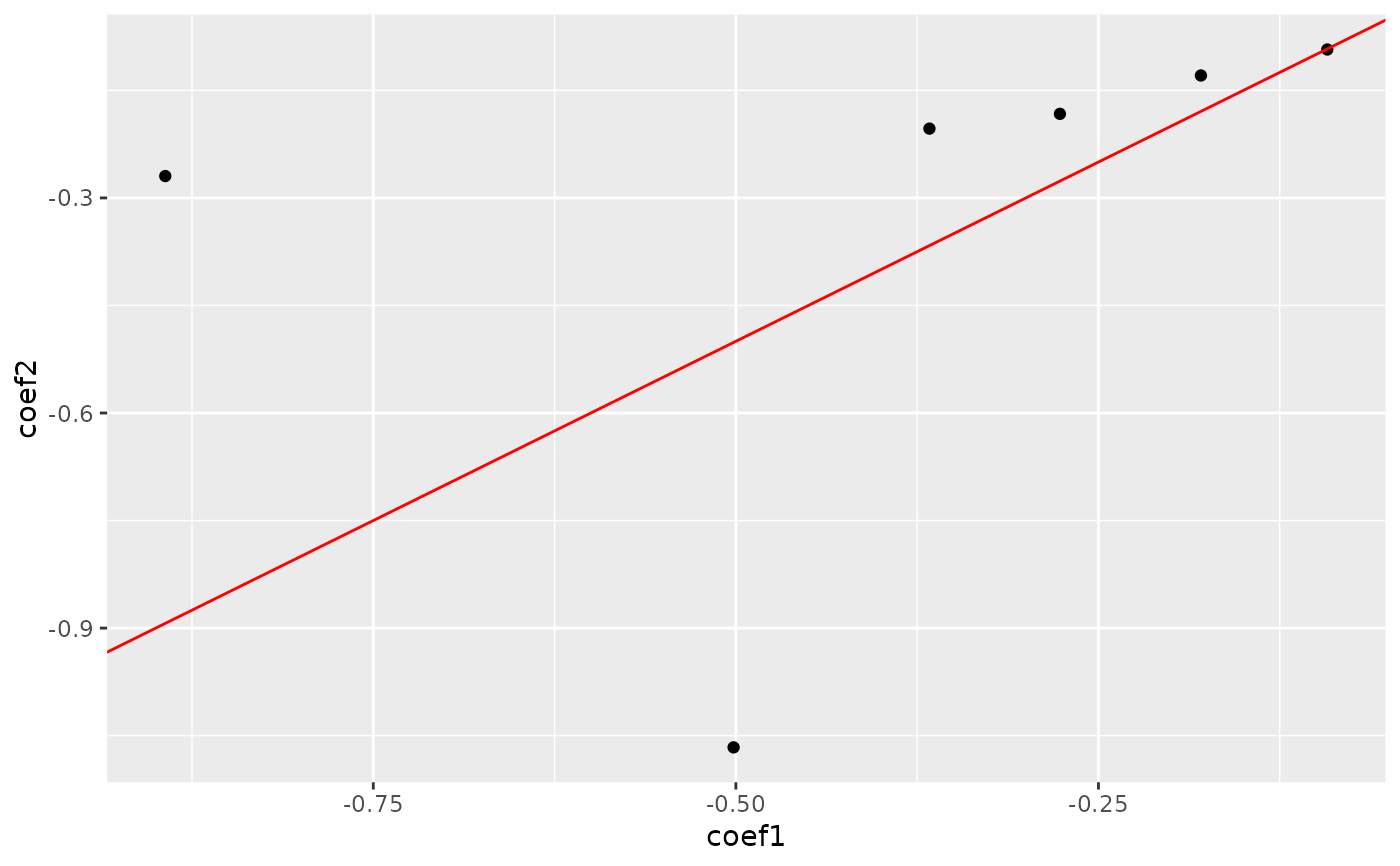#> $data
#> # A tibble: 6 × 3
#>   coef_name   coef1   coef2
#>   <fct>       <dbl>   <dbl>
#> 1 X01--X02  -0.0922 -0.0930
#> 2 X01--X04  -0.502  -1.07  
#> 3 X01--X09  -0.893  -0.269 
#> 4 X01--X11  -0.367  -0.203 
#> 5 X01--X13  -0.179  -0.129 
#> 6 X01--X18  -0.277  -0.183 
#> 
z1 = pairwise_col_diff(x1)
z2 = pairwise_col_diff(x2)
plot(predict_cpop(cpop_result, newz = z1)$cpop_model_avg,
predict_naive_glmnet(lasso_result, newz = z1)$naive_glmnet_avg)
#> Warning: The `newz` argument is now deprecated in preference for `newx`,
#>     CPOP prediction can still run.
abline(a = 0, b = 1, col = "red")