
APproximated Exhaustive Search (APES) is a model selection method for Generalised Linear Models. The accompanying paper is Wang et. al. (2019). You can find the vignette here.
A quick example
Suppose we have simulated a data with 500 rows and 20 predictor variables, and we have fitted a logistic regression model against a binary response variable. We may wish to perform an exhaustive variable selection on such a model to determine which variables produce the most parsimonious model. However, performing an exhaustive variable selection means looking through (2^{20} = 1,048,576) models! Exhaustive variable selection is known to be time consuming, and looking at so many models might take a long time.
APES is a variable selection method that first converts the logistic model into a linear model and then it uses a best-subset algorithm (such as leaps or mixed integer optimisation) to search for the best linear model. The selected linear models are then converted into logistic models. The reason for doing this is that the exhaustive variable selection can be performed much faster in the linear model space.
The current implementation of APES supports logistic, Poisson and Cox regression models.
library(APES)
## Simulating data
set.seed(123)
n = 500
p = 20
k = 1:p
beta = c(1, -1, rep(0, p-2))
x = matrix(rnorm(n*p), ncol = p)
colnames(x) = paste0("X", 1:p)
y = rbinom(n = n, size = 1, prob = expit(x %*% beta))
data = data.frame(y, x)
## Fitting a full model
model = glm(y ~ ., data = data, family = "binomial")
## Running APES selection
apes_result = apes(model = model)
apes_result
#> Time taken: 0.0002061009 minutes
#>
#> APES - AIC selected the following variables
#> intercept X1 X2 X3 X4 X5 X6 X7
#> 0.064 1.226 -1.093 0.000 0.000 0.000 0.000 0.000
#> X8 X9 X10 X11 X12 X13 X14 X15
#> 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
#> X16 X17 X18 X19 X20
#> 0.000 0.000 0.000 0.000 0.000
#>
#> APES - BIC selected the following variables
#> intercept X1 X2 X3 X4 X5 X6 X7
#> 0.082 1.284 -1.137 0.000 -0.161 0.000 0.000 0.000
#> X8 X9 X10 X11 X12 X13 X14 X15
#> 0.000 0.000 0.000 0.221 0.000 0.252 -0.162 0.000
#> X16 X17 X18 X19 X20
#> 0.208 0.000 0.000 0.000 0.000The best model of each model size are stored and the “best” model of all can be selected using an information criterion such as the Akaike Information Criterion (AIC) or the Bayesian Information Criterion (BIC). Notice how in the above output of APES, the true model size is identified as 3 and 2 by the AIC and BIC, respectively. The selected model estimates are also shown.
The bootstrap procedure can be used to understand the variable selection stability. The APES package also comes with some plotting functions that displays the bootstrapped results.
boot_result = apes(model = model, n_boot = 20)
boot_result
#> Time taken: 0.02650997 minutes
#> Total number of bootstrap APES results: 20
plot(boot_result, type = "vip")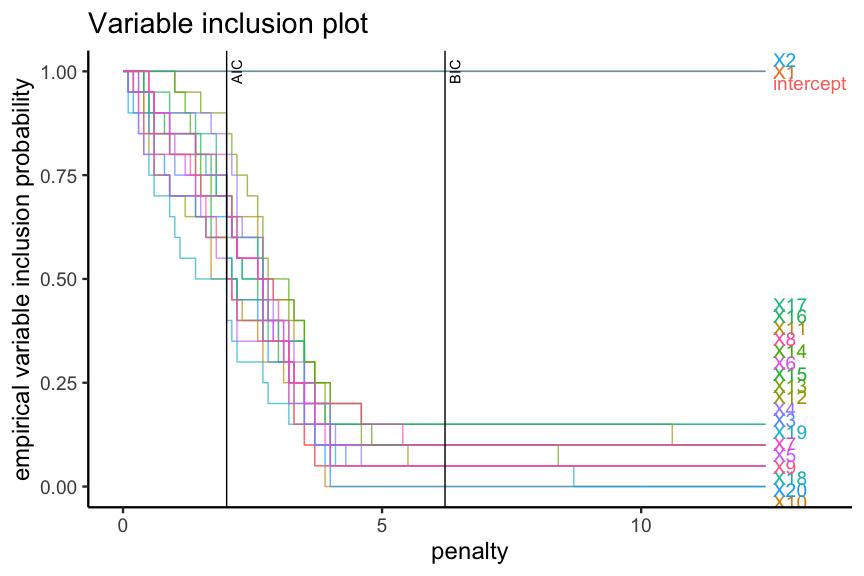
References
- Wang, K. Y., Tarr, G., Yang, J. Y., & Mueller, S. (2019). Fast and approximate exhaustive variable selection for generalised linear models with APES. Australian & New Zealand Journal of Statistics, 61(4), 445–465. https://doi.org/10.1111/anzs.12276