APES: birth weight data example
Kevin Y.X. Wang
School of Mathematics and Statistics, The University of Sydney, AustraliaGarth Tarr
School of Mathematics and Statistics, The University of Sydney, AustraliaJean Y.H. Yang
School of Mathematics and Statistics, The University of Sydney, AustraliaSamuel Mueller
Department of Mathematics and Statistics, Macquarie University, AustraliaSource:
vignettes/articles/birthweight.Rmd
birthweight.RmdIntroduction
In this vignette, we will demonstrate a real application of APES on a
logistic regression model. The data we have chosen is the birth weight
(birthwt) data from the MASS package. In this
data, there are 189 observations and the binary response variable is
whether an infant is in the low-weight group (low). There
are eight predictor variables in total comprising of two numeric
variables (age and lwt) and six others are
factor variables.
Loading packages and setting up the data
## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr 1.1.3 ✔ readr 2.1.4
## ✔ forcats 1.0.0 ✔ stringr 1.5.0
## ✔ ggplot2 3.4.4 ✔ tibble 3.2.1
## ✔ lubridate 1.9.3 ✔ tidyr 1.3.0
## ✔ purrr 1.0.2
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag() masks stats::lag()
## ✖ dplyr::select() masks MASS::select()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
data("birthwt", package = "MASS")
theme_set(theme_classic(14) +
theme(legend.position = "bottom"))We will simplify the data using the code below.
bwt <- with(birthwt, {
race <- factor(race, labels = c("white", "black", "other"))
ptd <- factor(ptl > 0)
ftv <- factor(ftv)
levels(ftv)[-(1:2)] <- "2+"
data.frame(low = factor(low), ## indicator for low-weight group
age, ## mother's age in years
lwt, ## mother's weight in pounds at last menstrual period
race, ## mother's race (white, black, other)
smoke = (smoke > 0), ## smoking status during pregnancy
ptd, ## indicator for previous premature labours
ht = (ht > 0), ## indicator for history of hypertension
ui = (ui > 0), ## indicator for uterine irritability
ftv ## number of physician visits during the first trimester
)
})
glimpse(bwt)## Rows: 189
## Columns: 9
## $ low <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ age <int> 19, 33, 20, 21, 18, 21, 22, 17, 29, 26, 19, 19, 22, 30, 18, 18, …
## $ lwt <int> 182, 155, 105, 108, 107, 124, 118, 103, 123, 113, 95, 150, 95, 1…
## $ race <fct> black, other, white, white, white, other, white, other, white, w…
## $ smoke <lgl> FALSE, FALSE, TRUE, TRUE, TRUE, FALSE, FALSE, FALSE, TRUE, TRUE,…
## $ ptd <fct> FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, F…
## $ ht <lgl> FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, F…
## $ ui <lgl> TRUE, FALSE, FALSE, TRUE, TRUE, FALSE, FALSE, FALSE, FALSE, FALS…
## $ ftv <fct> 0, 2+, 1, 2+, 0, 0, 1, 1, 1, 0, 0, 1, 0, 2+, 0, 0, 0, 2+, 0, 1, …Single run of APES on birthweight data
We will first fit a “full” logistic regression model utilising all available variables to get a preliminary understanding of the data and the model.
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.823 1.245 0.661 0.508
## age -0.037 0.039 -0.962 0.336
## lwt -0.016 0.007 -2.211 0.027
## raceblack 1.192 0.536 2.225 0.026
## raceother 0.741 0.462 1.604 0.109
## smokeTRUE 0.756 0.425 1.778 0.075
## ptdTRUE 1.344 0.481 2.796 0.005
## htTRUE 1.913 0.721 2.654 0.008
## uiTRUE 0.680 0.464 1.465 0.143
## ftv1 -0.436 0.479 -0.910 0.363
## ftv2+ 0.179 0.456 0.392 0.695While on the outset, many of these variables would have seem to have
an impact on the birth weight of an infant, the summary of the logistic
model (in particular the p-values) imply that some variables are
redundant. So we may wish to perform variable selection on this data
using the APES package with the main function being
apes.
apes_result = apes(model = full_model)## No variable size specified, searching all sizes from 1 to p...
apes_result## Time taken: 5.522569e-05 minutes
##
## APES - AIC selected the following variables
## intercept age lwt raceblack raceother smokeTRUE ptdTRUE htTRUE
## 0.095 0.000 -0.017 1.264 0.864 0.876 1.231 1.767
## uiTRUE ftv1 ftv2+
## 0.000 0.000 0.000
##
## APES - BIC selected the following variables
## intercept age lwt raceblack raceother smokeTRUE ptdTRUE htTRUE
## -1.057 0.000 0.000 0.000 0.000 0.000 1.463 0.000
## uiTRUE ftv1 ftv2+
## 0.000 0.000 0.000The apes_result gives us an indiaction as to which
variables are considered to be the most important by the Akaike
Information Criterion (AIC) and the Bayesian Information Criterion (BIC)
under an approximated exhaustive search. Note that APES handles a factor
variable in similar style as other R packages by
(alphabetically) selecting a level in the factor as the reference level
and compare all other levels against this reference.
Variable selection stability
Suppose we are using the BIC as the main selection criterion, a
single application of APES suggests that we should only select the
ptd variable. However, previous
studies into this data suggested that this data possess several
interesting characteristics, one being variable selection instability.
This means that the variables we select based on a single application of
any model selection method cannot always be reproduced if the data is
slightly perturbed. One way we can confirm the existence of this
instability is to perform a bootstrap resampling of the observations,
this introduces a perturbation on the data which affects model
selection.
set.seed(2020)
boot_bwt = bwt[sample(1:nrow(bwt), nrow(bwt), replace = TRUE), ]
full_model2 = glm(low ~ ., family = binomial, data = boot_bwt)
round(summary(full_model2)$coef, 3)## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.382 1.194 0.320 0.749
## age -0.001 0.039 -0.038 0.970
## lwt -0.017 0.007 -2.518 0.012
## raceblack 1.238 0.515 2.404 0.016
## raceother 0.346 0.487 0.711 0.477
## smokeTRUE 0.824 0.433 1.901 0.057
## ptdTRUE 1.097 0.486 2.257 0.024
## htTRUE 1.602 0.832 1.926 0.054
## uiTRUE 0.819 0.483 1.695 0.090
## ftv1 -0.970 0.553 -1.754 0.079
## ftv2+ -0.194 0.458 -0.423 0.672
apes(full_model2)## No variable size specified, searching all sizes from 1 to p...## Time taken: 4.70082e-06 minutes
##
## APES - AIC selected the following variables
## intercept age lwt raceblack raceother smokeTRUE ptdTRUE htTRUE
## 0.614 0.000 -0.018 1.111 0.000 0.681 1.161 1.675
## uiTRUE ftv1 ftv2+
## 0.812 -0.996 0.000
##
## APES - BIC selected the following variables
## intercept age lwt raceblack raceother smokeTRUE ptdTRUE htTRUE
## 0.897 0.000 -0.016 1.054 0.000 0.000 1.423 0.000
## uiTRUE ftv1 ftv2+
## 0.000 -1.315 0.000We can see that when we perturb on the data, the p-value for the
ht variable increases from 0.008 to 0.054, which could
cause confusion if we take a naive approach to only select variables
with p-values < 0.05. Similarly, this perturbation also affects APES,
as we have now selected three extra variables under the BIC. Variable
selection stability is not a criticism of any specific methods, but
rather, it is an issue for data with ambiguous signals. We will describe
how the APES package uses bootstrap resampling to improve
variable selection stability in the next section.
Bootstrapping with the APES package
One way that we can improve variable selection stability is to apply
APES on many bootstrap resampling of the data and then
average the computed results. As the main motivation of APES is to make
exhaustive selection fast and it is therefore also ideally suited for
such a procedure which requires a large amount of computation.
Running the apes function with an extra argument
n_boot automatically invokes bootstrapping sampling on the
rows of the data. The returned object is a boot_apes class
object which stores all bootstrapped apes objects. This
class comes with generic print, summary and
plot methods, which make the interaction with such an
object much easier.
The summary method summarises the averaged selection
(empirical) probability of each variable for a given information
criterion. In the next section, we will explore the plot
generic methods for this object class.
boot_result = apes(full_model, n_boot = 100)## No variable size specified, searching all sizes from 1 to p...Variable importance plot
The variable importance plot is a technique explored in Murray et.
al. (2013) and it shows the stability of each variable as empirical
probability of selection against different penalty terms, assuming the a
general information criterion formulation $-2 + (p + 1) $, where \(\ell\) is the log-likelihood of a model,
\lambda is the penalty term and \(p\) is the number of predictors (excluding
the intercept term). The most important difference between this
plot method and the
summary/method methods is that we are no
longer fixated on a single information criterion such as the AIC (where
\(\lambda = 2\)) and the BIC (where
\(\lambda = \log(p)\)). Instead, we can
visualise the selection with ever increasing penalty term \(\lambda\). Variables with stronger
selection stability are those with high probabilities of selection with
increasingly higher levels of penalisation.
We can see that the variables in order of strength of stability are
ptd, ht and lwt.
plot(boot_result, type = "vip")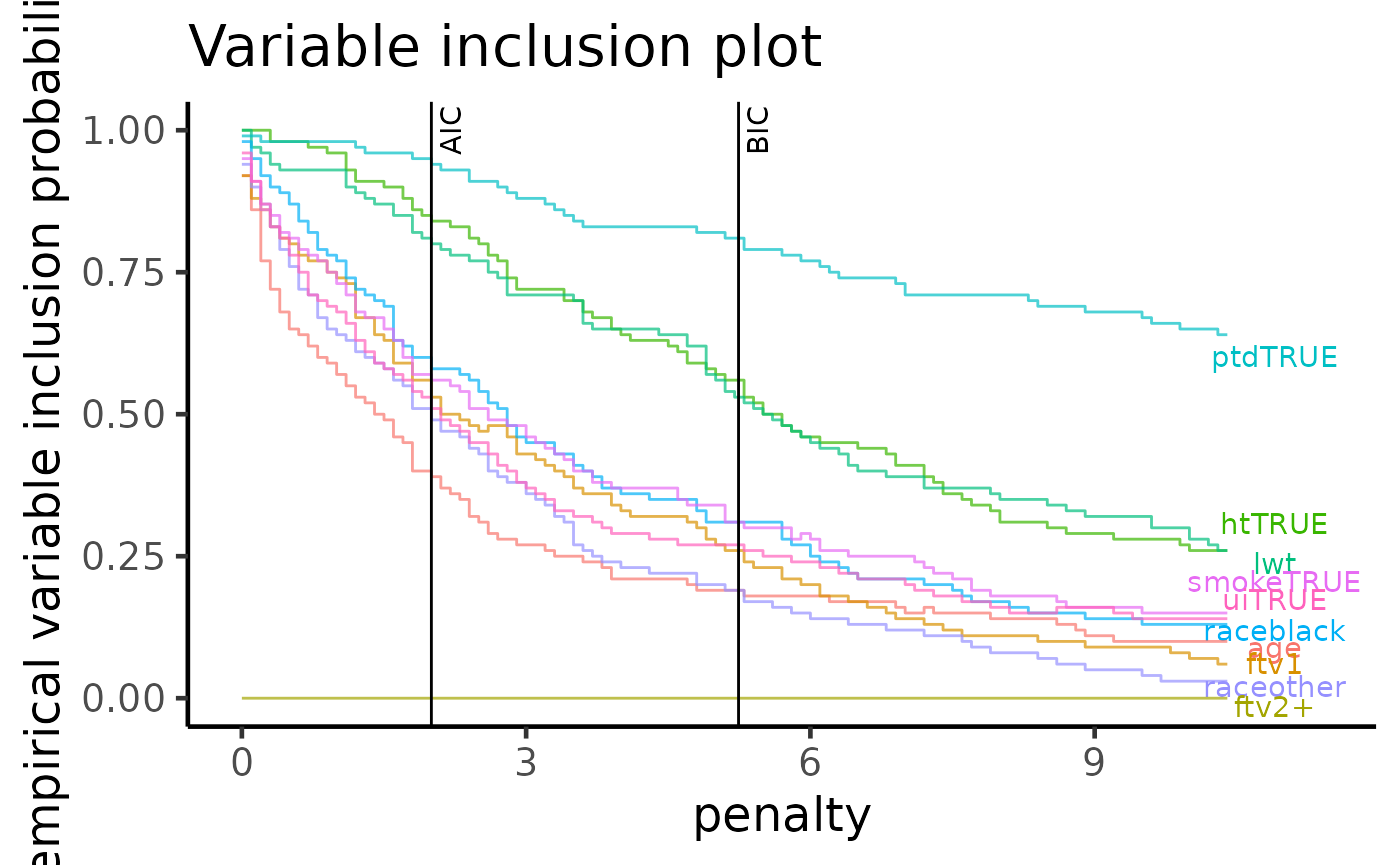
Tile version of VIP plot
This plot is identical in construction as the VIP plot above. However, the probability of selection is used as colours in a tile plot. The most stably selected variables are on the top of the y-axis.
plot(boot_result, type = "vip_tile")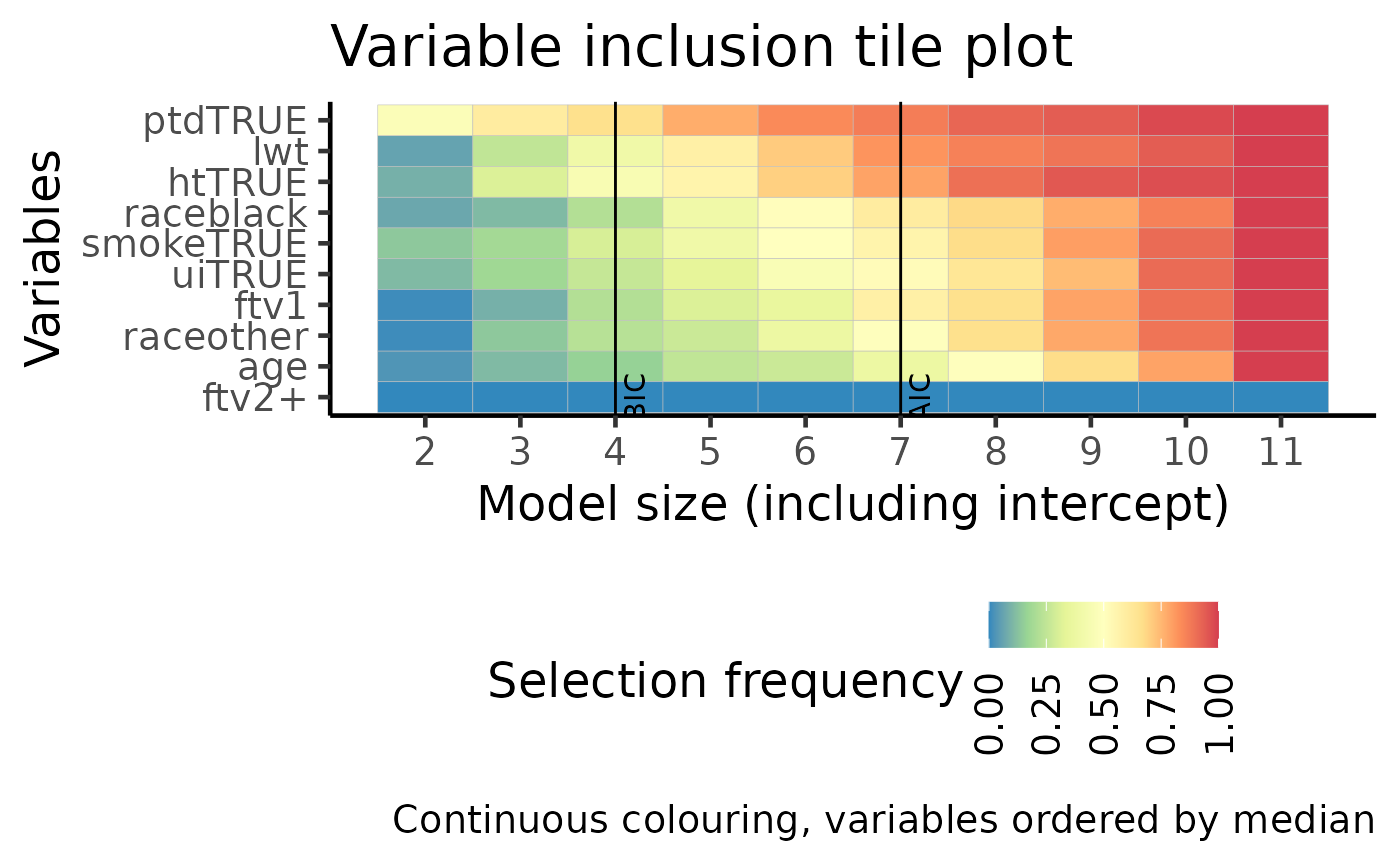
Model averaged coefficient plot
APES stores all the coefficient estimates in each bootstrap run. We can use this information to compute cumulative averages of variable coefficients. This plot allows us to examine the stability of the model coefficient estimates whereas the previous VIP plots shows only the stability of variable selection.
plot(boot_result, type = "ma")## Warning: Removed 1 rows containing missing values (`geom_text_repel()`).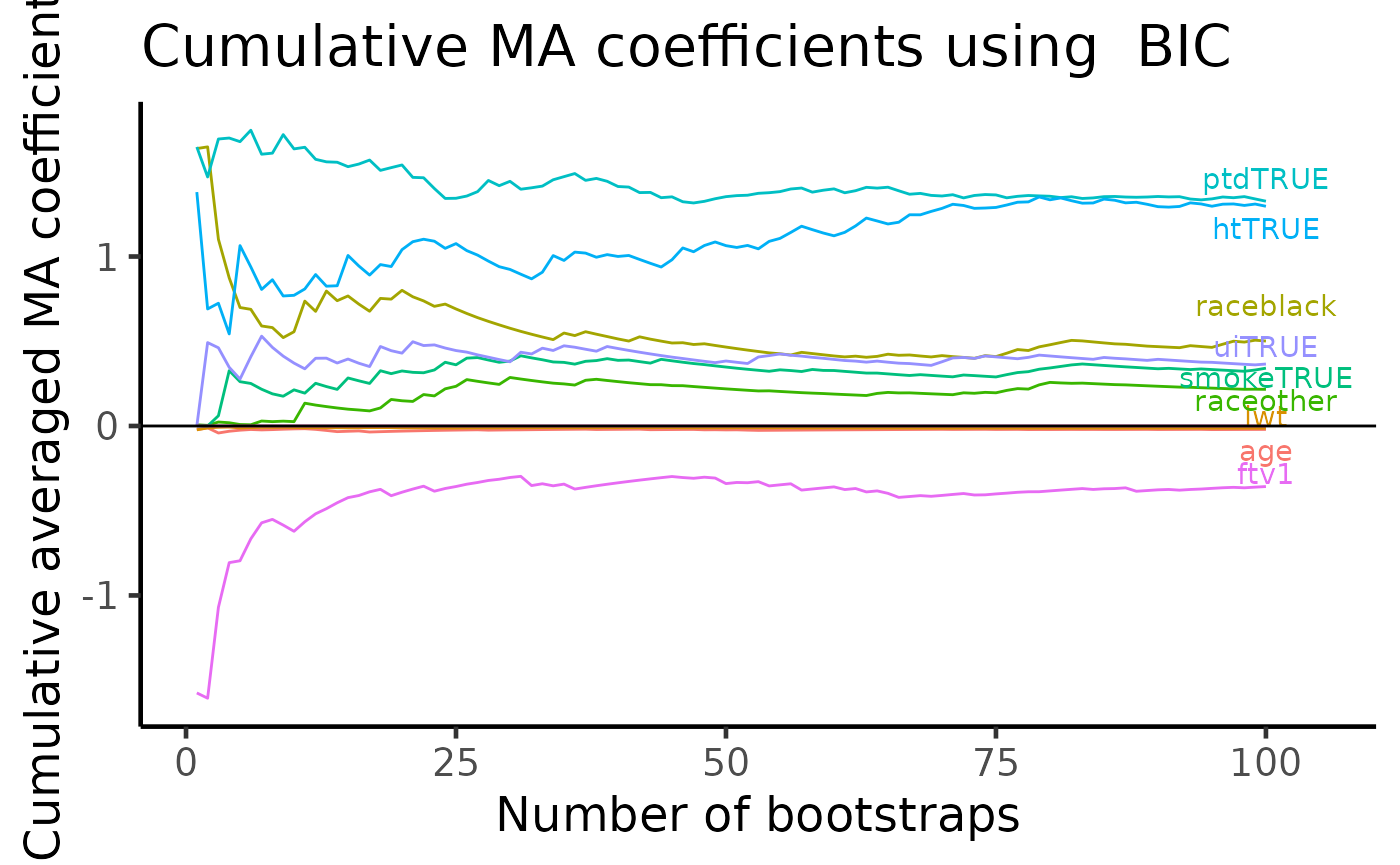
Information criterion pathway plot
During the bootstrap computations, APES records the best AIC/BIC models across all bootstrap runs. Due to the induced perturbation, the AIC/BIC-best model in each bootstrapped data do not always coincide. One way to examine the differences between these models is to look into the model size of the best selected model.
Here, each bootstrap run is represented by a black curve with the BIC-selected model of each run coloured as red. We can see that it is rare for a model of size 2 to be selected when using the BIC, with the majority of the models being between 3 and 6 in model size. This is a reason why we should perform such a bootstrap procedure to examine the model selection stability as a single run of APES only identifies a model of size two under the BIC selection criterion.
plot(boot_result, type = "path", order = "BIC")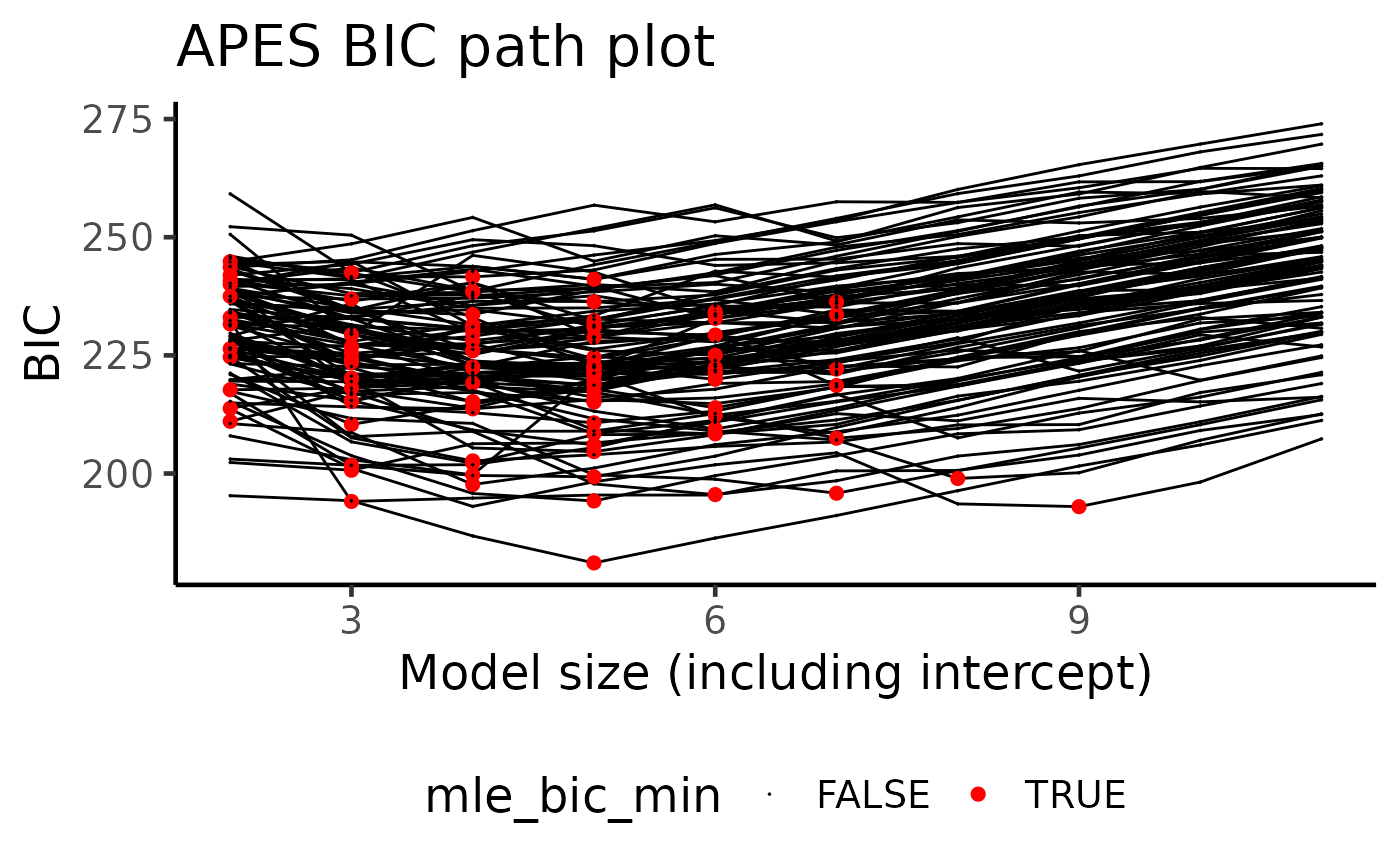
Parallel processing
For large number of bootstrap runs, one might consider using parallel
processing to reduce the total computational time. The parallel backend
support of APES uses the furrr package. To
invoke parallel processing, this requires a single parameter
workers.
parallel_result = apes(model = full_model, n_boot = 100, workers = 2)
parallel_resultReference
Mueller, S. and Welsh, A. H. (2010), On model selection curves. International Statistical Review, 78:240-256. doi: 10.1111/j.1751-5823.2010.00108.x
Murray, K., Heritier, S. and Mueller, S. (2013), Graphical tools for model selection in generalized linear models. Statistics in Medicine, 32:4438-4451. doi: 10.1002/sim.5855
Tarr G, Mueller S and Welsh AH (2018). mplot: An R Package for Graphical Model Stability and Variable Selection Procedures. Journal of Statistical Software, 83(9), pp. 1-28. doi: 10.18637/jss.v083.i09
Wang, K. Y., Tarr, G., Yang, J. Y., & Mueller, S. (2019). Fast and approximate exhaustive variable selection for generalised linear models with APES. Australian & New Zealand Journal of Statistics, 61(4), 445–465. https://doi.org/10.1111/anzs.12276
Session Info
## R version 4.3.2 (2023-10-31)
## Platform: x86_64-pc-linux-gnu (64-bit)
## Running under: Ubuntu 22.04.3 LTS
##
## Matrix products: default
## BLAS: /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3
## LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.20.so; LAPACK version 3.10.0
##
## locale:
## [1] LC_CTYPE=C.UTF-8 LC_NUMERIC=C LC_TIME=C.UTF-8
## [4] LC_COLLATE=C.UTF-8 LC_MONETARY=C.UTF-8 LC_MESSAGES=C.UTF-8
## [7] LC_PAPER=C.UTF-8 LC_NAME=C LC_ADDRESS=C
## [10] LC_TELEPHONE=C LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C
##
## time zone: UTC
## tzcode source: system (glibc)
##
## attached base packages:
## [1] stats graphics grDevices utils datasets methods base
##
## other attached packages:
## [1] lubridate_1.9.3 forcats_1.0.0 stringr_1.5.0 dplyr_1.1.3
## [5] purrr_1.0.2 readr_2.1.4 tidyr_1.3.0 tibble_3.2.1
## [9] ggplot2_3.4.4 tidyverse_2.0.0 MASS_7.3-60 APES_1.0.0
##
## loaded via a namespace (and not attached):
## [1] gtable_0.3.4 xfun_0.41 bslib_0.5.1 ggrepel_0.9.4
## [5] lattice_0.21-9 tzdb_0.4.0 vctrs_0.6.4 tools_4.3.2
## [9] generics_0.1.3 parallel_4.3.2 fansi_1.0.5 highr_0.10
## [13] pkgconfig_2.0.3 Matrix_1.6-1.1 RColorBrewer_1.1-3 desc_1.4.2
## [17] lifecycle_1.0.3 farver_2.1.1 compiler_4.3.2 textshaping_0.3.7
## [21] munsell_0.5.0 leaps_3.1 codetools_0.2-19 htmltools_0.5.6.1
## [25] sass_0.4.7 yaml_2.3.7 pillar_1.9.0 pkgdown_2.0.7
## [29] furrr_0.3.1 jquerylib_0.1.4 cachem_1.0.8 parallelly_1.36.0
## [33] gtools_3.9.4 tidyselect_1.2.0 digest_0.6.33 stringi_1.7.12
## [37] future_1.33.0 reshape2_1.4.4 listenv_0.9.0 labeling_0.4.3
## [41] splines_4.3.2 rprojroot_2.0.3 fastmap_1.1.1 grid_4.3.2
## [45] colorspace_2.1-0 cli_3.6.1 magrittr_2.0.3 survival_3.5-7
## [49] utf8_1.2.4 withr_2.5.2 scales_1.2.1 timechange_0.2.0
## [53] rmarkdown_2.25 globals_0.16.2 ragg_1.2.6 hms_1.1.3
## [57] memoise_2.0.1 evaluate_0.23 knitr_1.45 rlang_1.1.1
## [61] Rcpp_1.0.11 glue_1.6.2 jsonlite_1.8.7 plyr_1.8.9
## [65] R6_2.5.1 systemfonts_1.0.5 fs_1.6.3